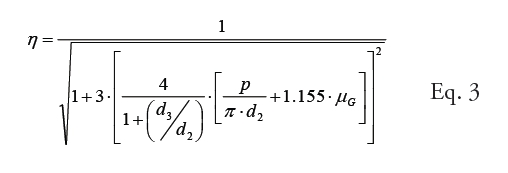Artigos
A que se propõem os Elementos de Fixação?
O tema discorre sobre o que são e qual a importância de peças tão essenciais, muitas delas vendidas aos quilos, como numa feira livre
 Denominamos Elementos de Fixação a qualquer “peça” cuja função/missão é “fixar alguma coisa numa outra coisa”. Nessa categoria podemos citar os Anéis Elásticos, as Abraçadeiras, os Pinos, as Porcas, os Prisioneiros, os Rebites, entre outros. O mais popular é o Parafuso, cuja aplicação pode ir desde implantes dentários até pontes, artefatos aeroespaciais, etc, mas esta “peça” sempre é considerada insignificante, pois, na grande maioria das vezes não possui valor agregado, é comercializada por “quilo” ou “cento”, ou seja, “por baciada”. Também nos projetos, é quase sempre a última a ser dimensionada. Denominamos Elementos de Fixação a qualquer “peça” cuja função/missão é “fixar alguma coisa numa outra coisa”. Nessa categoria podemos citar os Anéis Elásticos, as Abraçadeiras, os Pinos, as Porcas, os Prisioneiros, os Rebites, entre outros. O mais popular é o Parafuso, cuja aplicação pode ir desde implantes dentários até pontes, artefatos aeroespaciais, etc, mas esta “peça” sempre é considerada insignificante, pois, na grande maioria das vezes não possui valor agregado, é comercializada por “quilo” ou “cento”, ou seja, “por baciada”. Também nos projetos, é quase sempre a última a ser dimensionada.
Esta insignificância cai por terra quando um Parafuso não cumpre sua função. É uma realidade experimentada por todos nós: só damos valor para algo, quando o perdemos. Estima-se que o Parafuso é responsável por mais de 80 % dos recalls que ocorrem na indústria automobilística. E a causa vai desde a má definição do Parafuso para a aplicação específica, passando por problemas de qualidade, processos de aperto, etc.
Citando a sabedoria popular, podemos dizer que o limiar entre um indivíduo normal, em relação às suas faculdades mentais é um Parafuso, pois se diz que uma pessoa “tantã” tem um Parafuso a menos. Por que um Parafuso e não um Pino ou uma Porca? Também no gestual, faz-se um movimento com o dedo indicador apontando para as têmporas, girando (no sentido horário) informando ao interlocutor que estamos falando de um “tantã”, ou seja, refere-se não só ao Parafuso como que também a uma possível falta de aperto. Por observação pessoal, notei que este gesto é mundial (para os destros). Os canhotos fazem o mesmo gesto, porém girando no sentido anti-horário (possivelmente está apertado demais).
Não por acaso, nos parágrafos acima (e nos próximos)sempre será grafado o Elemento de Fixação coma primeira letra maiúscula, por exemplo, Parafuso, pois aqui ele e seus similares, como sujeitos, terão nomes próprios e consequentemente têm as suas responsabilidades e identidades particulares bem definidas.
Antes de detalhar as propriedades dos Parafusos, vamos discorrer sobre as Porcas, um dos poucos Elementos de Fixação com gênero feminino e nada mais coerente, pois “elas” sempre são mais resistentes que “eles”.
Os esforços inerentes às Porcas sempre serão de ordemaxial, logo o conceito de Resistência a Tração (EsforçoAxial) reflete bem a natureza deste Elemento de Fixação. Dependendo do Grau de Resistência da Porca, é necessário tratamento térmico.
Na Tabela 1, temos os valores mínimos de Tração de Teste, em N/mm² (ou MPa, no Sistema Internacional),em função do diâmetro nominal.
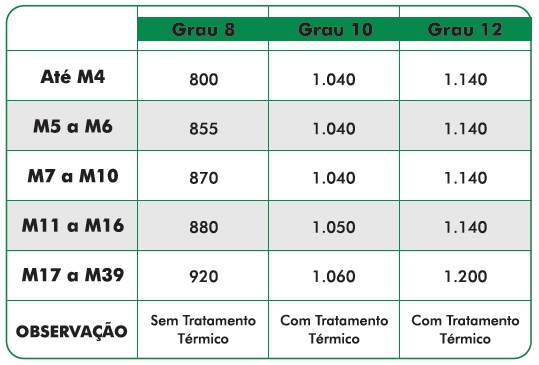
Tabela 1 - Tração de Teste (MPa) em relação à dimensão de Porca e do Grau de Resistência
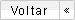
Outras características mecânicas são mostradas na Tabela 2, em função do Grau de Resistência.
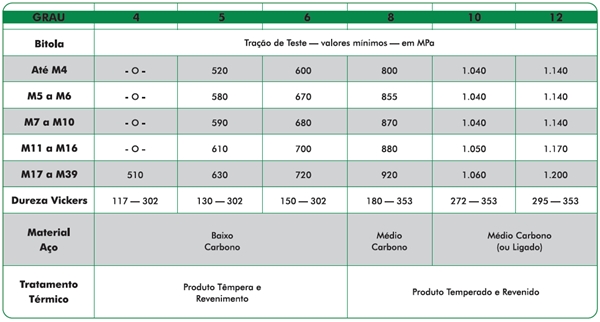
Tabela 2 – Características mecânicas em relação à dimensão da Porca e do Grau deResistência
Os valores de Tração de Teste devem ser convertidos em Força, para um melhor entendimento da capacidadede um Elemento de Fixação. Desta forma, temos que considerar os fatores geométricos, como por exemplo,a bitola e o passo, a fim de calcular a referida capacidade. Para converter Tração calcular a área resistiva (As) do Elemento de Fixação. A Equação 1 é válida para séries de roscas Normal e Fina.
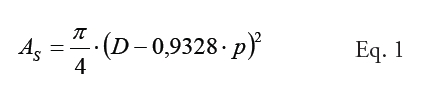
onde D = diâmetro nominal do Elemento de Fixação
p = passo
Na Tabela 3, temos alguns exemplos com os respectivos valores de Força Axial (em k N), para os diversos Graus de Resistência, calculados a partir da mínimaTração de Teste.
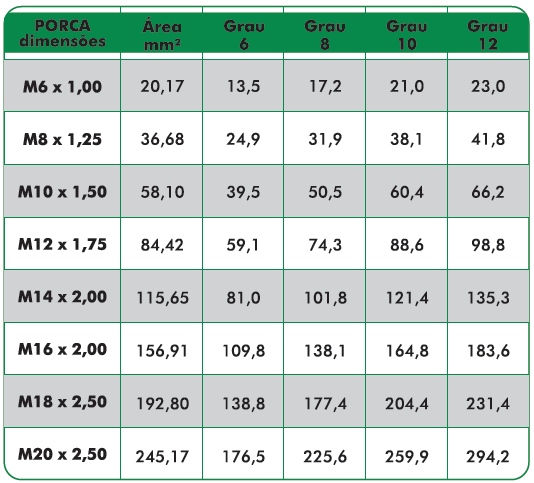
Tabela 3 - Valores de força Axial, em KN, para diversas Porcas com diferentes Graus de Resistência.
Os valores mostrados na Tabela 3 indicam qual é a mínima capacidade de Força Axial suportada por uma Porca, considerando sua dimensão e o respectivo Grau de Resistência.
Como já ressaltado, “ela” é, na maioria das vezes, a “peça” mais resistente do que “ele” e estes valores podem ser comparados com a Capacidade de Geração de Força do Parafuso (“ele”), assumindo o Esforço Combinado (Tração – Torção), assinalados na Tabela 6.
Com relação aos Parafusos, a classificação da Resistência segue uma terminologia particular. Os Parafusos utilizados pela indústria automobilística, por exemplo, são identificados como: Classe 4.8, 5.8, 6.8, 8.8, 10.9 e 12.9. Os Parafusos Classe 4.8, 5.8 e 6.8 não sofrem tratamento térmico. Já os Parafusos Classe 8.8, 10.9 e 12.9 precisam de tratamento térmico (têmpera e revenimento). Existe também a Classe 9.8, que não é mais utilizada em projetos novos, por estar em fase de extinção em algumas montadoras. O significado destes números pode ser descrito, para uma melhor compreensão,observando a Figura 1, que se refere a um Parafuso com Classe de Resistência 8.8:
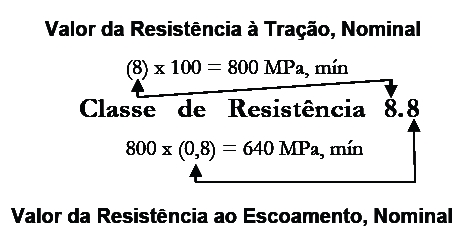
Figura 1 – Descrição de um Parafuso segundo sua de Resistência, no caso, 8.8.
Analogamente, os valores nominais para Parafusos de cada Classe de Resistência são mostrados na tabela abaixo:
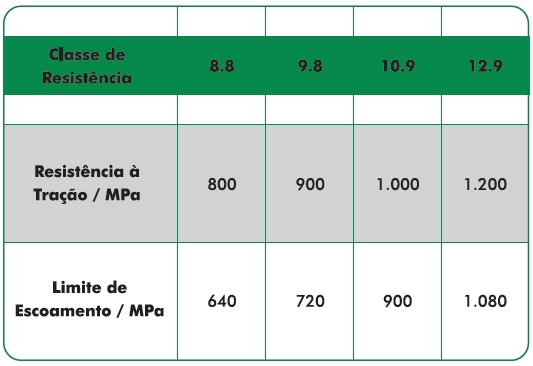
Tabela 4 – Valores nominais para Parafusos segundo sua Classe de Resistência
A especificação ISO 898 Parte I determina valores mínimos para o Limite de Resistência à Tração (LRT) e Limite de Escoamento (LE) para cada categoria de Parafuso. Também recomenda Dureza Rockwell “B” HR”B” (para Parafusos não tratados termicamente), Dureza Rockwell “C” HR”C” (para Parafusos temperados e revenidos). Seus respectivos valores são mostrados na tabela a seguir:
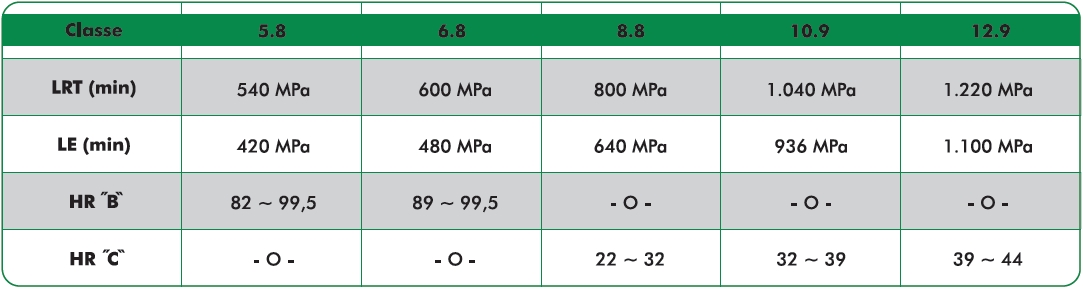
Tabela 5 - Valores mínimos para LRT, LE e dureza Rockwell para Parafusos, segundo sua Classe de Resistência.
Os Parafusos com as Classes de Resistência 4.8, 5.8 e 6.8 normalmente são confeccionados de Aço com Baixo ou Médio Carbono. Para os Parafusos com as Classes de Resistência 8.8, 10.9 e 12.9 o Aço deve ser Médio Carbono ou Aço Ligado.
O procedimento convencional para calcular a Capacidade de Geração de Força que se pode obter de um Parafuso requer conhecer as suas características geométricas e a Classe de Resistência. Assim, por exemplo, um Parafuso M12 × 1,5 Classe 10.9, possui Limite de Resistência à Tração (LRT) entre 1.040 e 1.220 MPa, uma vez que o limite superior da Classe 10.9 é o limite inferior da Classe imediatamente acima, no caso 12.9, e seu valor nominal igual a 1.000 MPa. Neste caso o M representa o sistema métrico e o 12 refere-se ao diâmetro nominal do Parafuso (12 mm). O número 1,5 representa o passo, ou seja, a distância existente entre as cristas de dois filetes consecutivos, no caso, 1,5 mm. A Força que este Parafuso suportará sem ruptura é dada pela Equação 2:
.jpg)
O LRT varia entre 1.040 e 1.220 MPa e a área resistiva deste Parafuso é de 88,1 mm², segue então que:
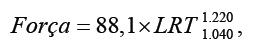
ou seja, a Força que se pode obter deste Parafuso está entre 91,6 kN e 107,5 kN. Considerando o Limite de Escoamento (LE) na fórmula da Força (eq. 2) conclui-se que este Parafuso começa a escoar entre 82,5 kN e 96,7 kN. Devemos lembrar que estes valores referem-se à Força Axial (tração pura). Todavia, num processo de aperto tem-se um Esforço Combinado, pois simultaneamente ocorrem esforços axiais e torsionais. O comportamento do Parafuso durante este processo de aperto – bem como as distintas regiões de Forças que se obtém dele, considerando o seu Grau de deformação – pode ser visto na Figura 2, abaixo:
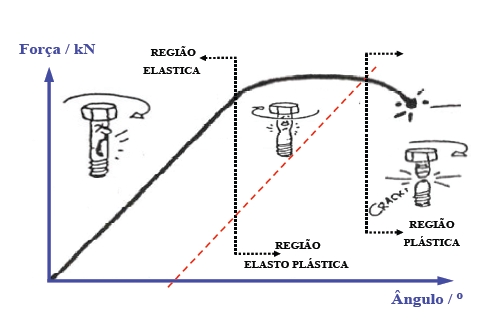
Figura 2 – Gráfico Força (de união) em relação ao aperto (em ângulo) do Parafuso
Na região denominada “elástica”, o Parafuso se comporta como se fosse uma mola, isto é, o comportamento é linear e a deformação não é permanente. Assim, se parar de apertar, ao desapertar, o Parafuso retornará às suas dimensões originais, respeitando a Lei de Hooke. O limiar da zona elástica define o Limite de Escoamento e este valor também é conhecido como Yield Point. A partir de uma dada Força, começa o processo de deformação permanente em associação ao alongamento do Parafuso e neste ponto entra-se na região denominada “elasto-plástica”, ou seja, o Parafuso está em uma zona de deformação que é parcialmente permanente. Ao desapertar este Parafuso, o seu comprimento será maior que o original, mas ainda não há estricção considerável. Ao final da zona elasto-plástica, chega-se à máxima deformação permanente, entrando na região “plástica”, onde o Parafuso está nas proximidades do seu limite de ruptura, condição inaceitável em qualquer processo de aperto.
Na Figura 2 observa-se a Força (em kN) em função do Aperto (ângulo, em graus). Nesta estratégia, considera- se o Esforço Combinado tração – torção e, desta forma, os valores de Força sofrem certa redução percentual. Esta redução, que denominamos Rendimento (η), por sua vez, é função exclusiva do coeficiente de atrito de rosca (μG) e é dada pela Equação 3:
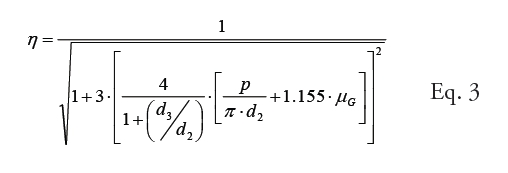
onde:
p (passo), d2 (diâmetro primitivo da rosca do Parafuso) e d3 (diâmetro do núcleo da rosca do Parafuso), que são os parâmetros geométricos do Parafuso considerado.
Esta equação revela que o rendimento é inversamente proporcional ao Coeficiente de Atrito de Rosca (μG), ou seja, quanto menor μG, maior será o rendimento (η).
Exemplificando para um Parafuso M12 × 1,5 (passo fino), com Classe de Resistência 10.9, assumindo que o Coeficiente de Atrito de Rosca está numa faixa de 0,10 ≤ μG ≤ 0,16, tem-se o rendimento variando entre 86,7 % a 77,2 %. Assim, o Limite de Resistência à Tração, que no esforço axial era de 91,6 a 107,5 kN, agora passa a ser de 70,7 a 93,2 kN respectivamente, considerando o Esforço Combinado, ou seja, contemplando o menor rendimento para a menor Resistência à Tração (1.040 MPa) e o maior rendimento para a maior Resistência a Tração (1.220 MPa). De maneira similar, o Limite de Escoamento, que se situava entre 82,5 e 96,7 kN, agora se encontra entre 63,7 e 83,9 kN. Estes números indicam qual é a faixa real de trabalho de um Parafuso M12, passo 1,5, com Classe de Resistência 10.9, quando assumimos somente a região elástica (e 0,10 ≤ μG ≤ 0,16).
Desta forma, para se calcular a Capacidade de Geração de Força de um Parafuso, na zona elástica, devemos considerar: I) O Limite de Resistência à Tração (máximo e mínimo); II) A Área Resistiva, que é função do passo e da bitola do Parafuso; III) O Rendimento, que é função exclusiva do Coeficiente de Atrito de Rosca (μG), nos seus limites máximo e mínimo e IV) Quanto ao Limite de Escoamento, considerar a Classe de Resistência, aplicando 80 % do Limite de Resistência à Tração para 8.8 e 90 % para 10.9 e 12.9.
Um sumário dos valores de Força, capaz de ser gerada por um Parafuso, passo normal, considerando o limiar da zona elástica (Yield Point), assumindo o Coeficiente de Atrito de Rosca numa faixa de 0,10 ≤ μG ≤ 0,16 e aplicando 80 % do Limite de Resistência à Tração para 8.8 e 90 % para 10.9 e 12.9 é mostrado na Tabela 6.
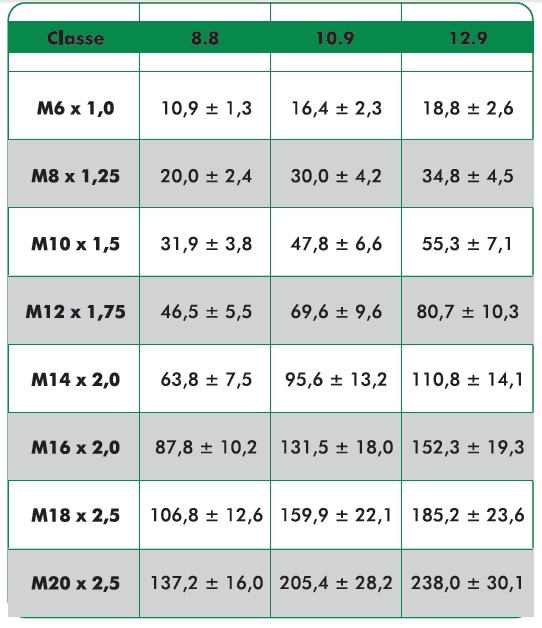
Tabela 6 – Valores de Força (em k N) e a respectiva dispersão, considerando a zona elástica de um Parafuso, segundo sua Classe de Resistência e 0,10 ≤ μG ≤ 0,16
Os valores apresentados na Tabela 6, considerando o Esforço Combinado, são referentes ao Limite de Escoamento e a dispersão é em função da faixa especificada para o Limite de Resistência à Tração bem como assumindo o Coeficiente de Atrito de Rosca numa faixa de 0,10 ≤ μG ≤ 0,16.
De maneira conservadora, usualmente se utiliza apenas 75 % destes valores.
A parte final deste artigo será publicada em nossa próxima edição.
Dr. Roberto Garcia
Consultor técnico, bacharel em química, mestre e doutor em físico química pela UNESP (Universidade Estadual Paulista).
roberto.2.garcia@gmail.com
|
 Edições on-line
Edições on-line  Fale Conosco
Fale Conosco 



 CONTEÚDO DA EDIÇÃO
CONTEÚDO DA EDIÇÃO




 Edição 102
Edição 102


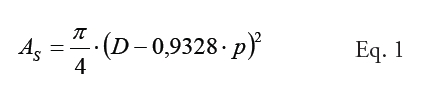




.jpg)