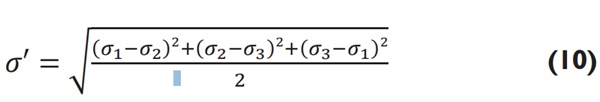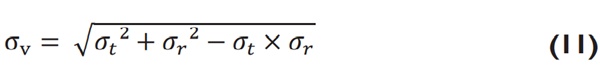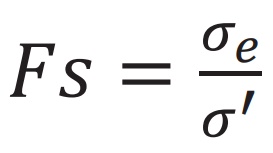Artigos 

Análise teórica de tensões distribuidas em carcaça de matriz de forjamento a frio - Parte Final

Autor conclui estudo que busca elevar a eficiência na fabricação de fixadores por meio da ampliação da longevidade do ferramental

A teoria da energia de distorção (DE) - von Mises

O mecanismo de deformação é atualmente entendido como sendo causado pelo deslizamento de planos dentro de sua estrutura cristalina, devido a tensão de cisalhamento e é acompanhado pela distorção na forma da peça (Norton, 2013)

A teoria da energia de distorção prediz que o escoamento ocorre quando a energia de deformação por distorção em unidade de volume alcança ou excede a energia de deformação por distorção por unidade de volume no escoamento sob tração ou compressão simples do mesmo material. (Budynas, R. G. Nisbetl, J. K. 2011, p. 234).

No caso de tração simples o escoamento ocorre quando a tensão equivalente é igual ou excede a tensão de escoamento do material (σ≥σe).

Logo, para o estado geral de tensão, a tensão equivalente é usualmente chamada de tensão de von Mises (σ'). Assim o escoamento é predito quando σ'≥σe. A tensão de von Mises é expressa por: 

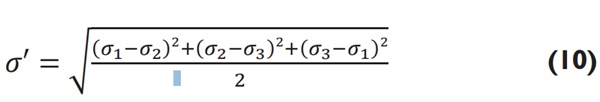
No qual σ1,σ2,σ3 são tensões principais.

Para o caso de tensão biaxial, para um cilindro pressurizado ou carcaça matriz, onde σ1 e σ2 são as tensões principais não nulas, a eq. (10) se resume a eq. (11), apresentada por Billigmann e Feldmann (1979, p. 326), como tensão de solicitação do material (σv), onde as tensões tangencial e radial assumem as tensões principais.

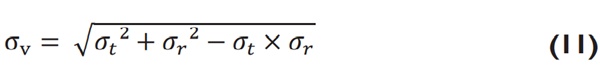
O fator de segurança para esta teoria pode ser expresso como:

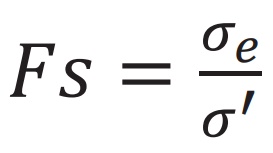
Onde:

= Fator de segurança [adimensional]

= Tensão de escoamento do material de análise [MPa]

= Tensão de von Mises [MPa]

 METODOLOGIA

O presente estudo abordou duas formas distintas para avaliar as tensões na carcaça da matriz, sendo simulação por meio de FEA (análise por elementos finitos), com o auxílio do software SolidEdge, e o cálculo analítico baseado na teoria de Lamé para cilindros de parede grossa.

No desenvolvimento do cálculo foi considerado o processo de recalque do blank da bucha cilíndrica, com comprimento inicial de ~17,5 mm e diâmetro inicial de 18,62 mm, conformado até o comprimento final de 13 mm e diâmetro de 21,60 mm.

A carcaça da matriz apresenta diâmetro externo de 130,18 mm e diâmetro interno de 45,50 mm. O núcleo/matriz tem diâmetro externo de 46 mm, conforme eq. (3), e diâmetro interno de 21,77 mm, antes da montagem. A interferência de montagem do conjunto, necessária ao forjamento da bucha foi definida conforme eq. (5).

A figura 5 ilustra esse processo, as composições químicas e propriedades mecânicas dos materiais envolvidos serão abordados nas seções a seguir.

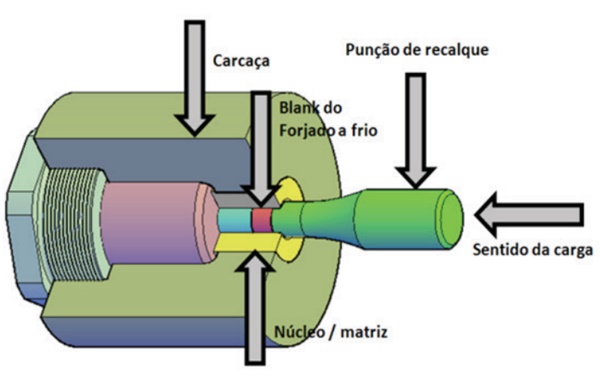
Figura 5: forjamento de uma bucha cilíndrica (autor, 2020)

Materiais de análise

O material adotado para o conformado (bucha) foi o AISI 5120 recozido, apontado por Button (1999, p.55) como aço de boa conformabilidade a frio. Sua resistência à deformação (kf) foi defi nida a partir do grau de deformação (φ) envolvido no processo e sua curva de fluência, baseado no exposto em Billigmann e Feldmann (1979, p. 526).

Sua composição química é exibida na tabela 1. 

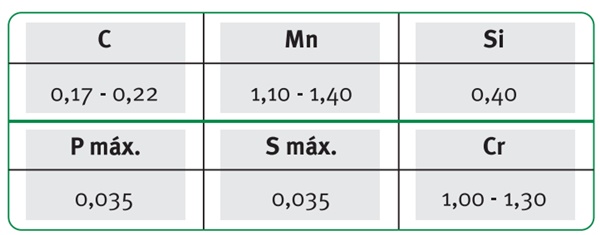
Tabela 1: composição química do aço AISI 5120 (Favorit, 2020).

Quanto ao ferramental, foi adotado o aço AISI H13 na dureza de 46 HRC para a carcaça e VWM2 na dureza de 60 HRC para o núcleo/matriz.

Suas composições químicas assim como as propriedades mecânicas são expostas a seguir.

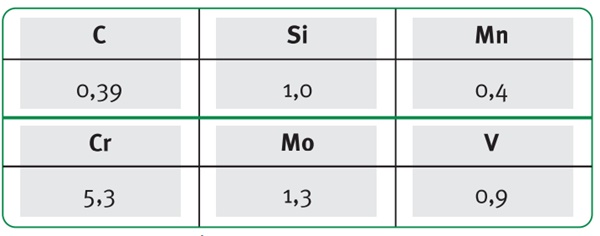
Tabela 2: composição química do aço AISI H13 (Yildiz, 2016).

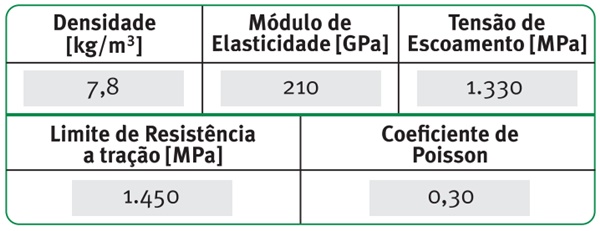
Tabela 3: propriedades mecânicas do aço AISI H13 com dureza de 46 HRC (Yildiz, 2016).

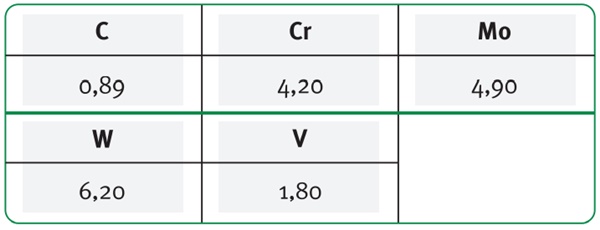
Tabela 4: composição química do aço VWM2 (Villares, 2019).

Tabela 5: propriedades mecânicas do aço VWM2 com dureza de 60 HRC (Gomes, 2019).

RESULTADOS E DISCUSSÕES

Considerando a operação de recalque a frio do blank da bucha cilíndrica eq. (1), e o coeficiente de atrito igual a 0,10, a tensão de recalque ou pressão interna "Pi" necessária a conformação é apresentada abaixo.

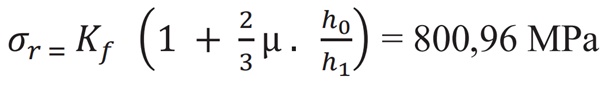
Os cálculos desenvolvidos com base nas eq. (4), eq. (5) e eq. (7), estabelecem a pressão de contato atuante na interface matriz-carcaça, no valor de 972,51 MPa.

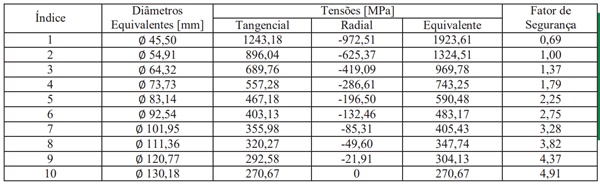
Tabela 6: resultados das tensões e fatores de segurança distribuídos através da parede da carcaça.

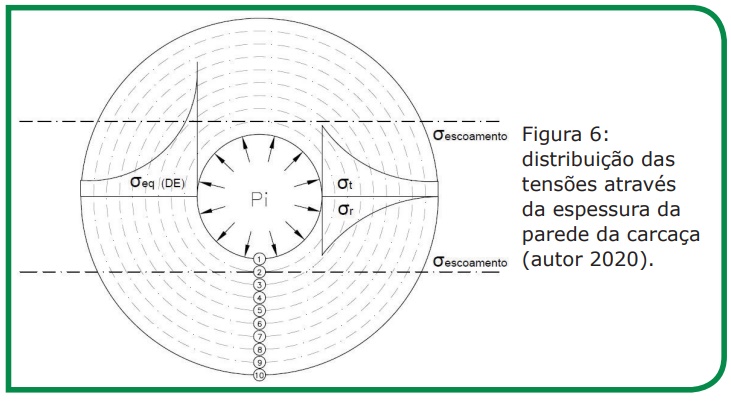
Considerando a carcaça da matriz como cilindro internamente pressurizado (pressão externa nula), os valores obtidos para as tensões radial, tangencial e equivalente, eq. (8), eq. (9) e eq. (11), assim como os fatores de segurança eq. (12), são apresentados na tabela 6. Os resultados apresentados foram obtidos a partir da divisão da parede da carcaça em dez diâmetros equivalentes, figura 6.

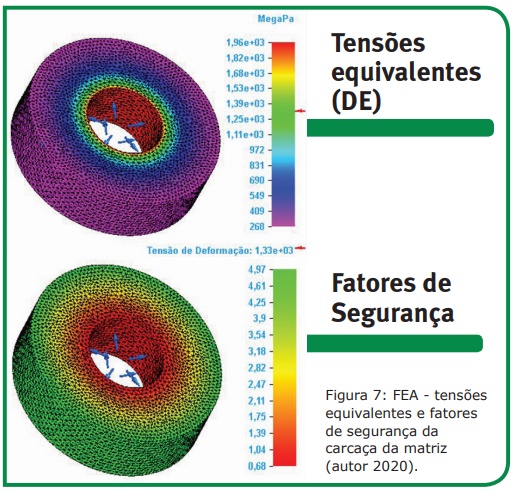
Na simulação em software foi adotada a mesma pressão de contato (972,51 MPa), mesmas características geométricas, físicas e mecânicas para a carcaça, os valores de tensão equivalente, juntamente com os fatores de segurança alcançados neste teste são apresentados na figura 7.

CONCLUSÃO

A partir da simulação e dos cálculos desenvolvidos, foi possível observar que na montagem e operação do ferramental em questão as tensões são máximas no diâmetro equivalente ao furo da carcaça, com valores que ultrapassam o limite elástico do material.

Na análise, a carcaça foi dividida em dez diâmetros equivalentes. Na interface de montagem foi observada a maior tensão equivalente, na ordem de 1900 MPa, reduzindo a aproximadamente 270 MPa no diâmetro externo da carcaça. Os fatores de segurança apresentaram comportamento inverso, apresentando valor mínimo de 0,69 na interface de montagem e 4,91 no diâmetro externo da carcaça.

Comparando os métodos de análise foi possível verificar variação aproximada de 2% tanto nas tensões equivalentes, quanto nos fatores de segurança, em seus extremos.

A partir dos valores dos coeficientes de segurança encontrados é possível observar que 20% da parede da carcaça falha por escoamento, enquanto o restante permanece dentro de valores aceitáveis com os coeficientes de segurança aumentando ao passo que o ponto de análise se afasta do furo da carcaça.

Como a pressão máxima ocorre na interface de montagem, ali também surgem altas tensões tangenciais, resistivas a tensão radial, favorecendo o surgimento de micro trincas na face interna da carcaça, logo este deve ser o ponto de maior atenção durante o processo de montagem.

AGRADECIMENTOS

O autor agradece aos professores da faculdade Una de Contagem, em especial ao MSc. Bruno Costa Chaves e a Dra. Fernanda Christina Teotônio Dias Troysi, pela orientação neste trabalho.

Agradece ainda aos amigos Wevilei Silva, Cássio Figueiredo, Saulo Fernandes, Hércules Lima, Sandro Aparecido, Celso Luís Coelho Bordignon, Anderson Rezende, Júlio Cesar dos Reis, Douglas Roberto Alves Fernandes, Crézio Alves da Silva, Raul Dangelis Marques e José Carlos Benatti, por contribuir e acreditar na realização dessa pesquisa.

REFERÊNCIAS

SUSKI, C. A.: "Conformação mecânica de múltiplos estágios", Florianópolis, SC, 2015.

PYTEL, Andrew; SINGER, L. Ferdinand: "Resistencia de Materiales", 4ª ed., México, Editora Harla, 1977.

COLLINS, J. A.: "Projeto Mecânico de Elementos de Máquinas - Uma Perspectiva de Prevenção da Falha", 1ª ed., Editora LTC, 2002.

JUVINALL, R. C.: "Stress, Strain and Strength", McGraw-Hill, Book Company, New York, 1967.

BUDYNAS, R. G.; NISBETT, J. K.: "Elementos de Máquinas de Shigley", 8ª ed., Porto Alegre, Editora Bokman, 2011.

NORTON, L. R. "Projeto de máquinas: Uma abordagem integrada", 4ª ed., Porto Alegre, Editora Bookman, 2013.

BILLIGMANN, J.; FELDMANN, H. D.: "Estampado y prensado a máquina", Editora Reverté, Barcelona, 1979.

BRAGA, A.: "Cilindros de Paredes Grossas: Solução de Lamé", Departamento de Engenharia Mecânica, PUC - Rio de Janeiro, disponível em http://abraga.usuarios.rdc.puc-rio. br/mecsol2/cilindros.pdf (acesso em 5 de outubro de 2019).

GOMES, L. S.: "Estudo comparativo entre o aço AISI M2 e o aço DIN 50 NICR13 no processo de conformação a frio", Universidade Presbiteriana Mackenzie, SP, 2019.

“Catálogo de Aços para Construção Mecânica - Villares Metals, 2019”, disponível em http://www.villaresmetals.com.br/pt/Produtos/Acos-Rapidos/VWM2 (acesso em 30 de dezembro de 2019).

Yildiz, H.: "A case study for improving tool life in cold forging: Carbon fiber composite reinforced dies", research on Engineering Structtures & Materials, disponível em http://jresm.org/archive/resm2016.24me2902. pdf (acesso em 21 de fevereiro de 2020).

BUTTON, S. T.: "Planejamento do processo e projeto de ferramentas para o forjamento a frio", São Paulo, SP, Unicamp, 1999.

“Aços Construção Mecânica – Favorit Aços Especiais”, disponível em http://www.favorit.com.br/produtos/acosconstrucao-mecanica/aco-din-20-mn-cr5-5120 (acesso em 11 de abril de 2020).

Genival Gonçalves Santos

Técnico mecânico, graduando em engenharia mecânica 1Faculdade UNA (Contagem, MG), o autor atua há mais de 17 anos na indústria de fixadores, 15 deles na Acument Brasil Sistemas de Fixação S.A., especificamente na planta industrial de Contagem, MG. Nessa empresa ele acumulou 11 anos de trabalho em ferramentaria, com produção e montagem de matrizes para fabricação de fixadores.

genivalgoncalves@hotmail.com