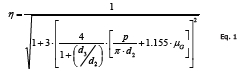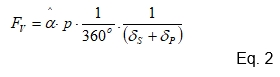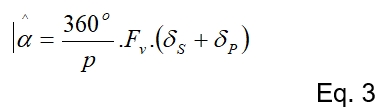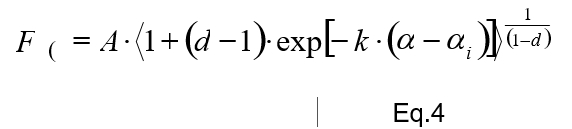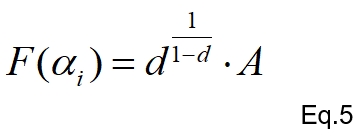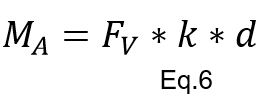Artigos

O parafuso no nosso cotidiano. Quanta Ciência e quanto menosprezo. Casos relatados de Recalls – Parte 1

Nesta edição e nas próximas abordaremos aqui como os elementos de fixação estão presentes em nosso dia-a-dia, sua abrangência de aplicações, das Ciências dos Materiais existentes nesses meros parafusos e porcas, e o quão os mesmos são menosprezados, bem como suas consequências 

Iniciaremos fazendo uma abordagem teórica, com vários aspectos físicos e matemáticos, e nas próximas edições exemplos serão apresentados, a fim de consolidar os conceitos teóricos aqui explanados. O roteiro a ser seguido envolverá Juntas, Capacidade de geração de Força por um Parafuso, Torque, Revestimentos, aspectos inerentes aos Coeficientes de Atrito e Processos de Aperto. Os exemplos contemplarão um parafuso, utilizado em aerogeradores, ou seja, nos sistemas Eólicos; um parafuso aplicado em veículos automotivos e na derradeira edição; um parafuso utilizado em implantes odontológicos. (Foto - Dr. Roberto Garcia)

Além das diversas bitolas - de M40 a M0,9 - os exemplos eleitos são de alta criticidade, tanto do ponto de vista de Projeto, dos materiais selecionados e dos processos de aperto. Encerrando esta matéria, um sumário de notificações de "recalls" envolvendo elementos de fixação.

Junta

Uma Junta basicamente é um trio (ou terno) que devem ser projetados harmoniosamente. O parafuso, o elemento roscado externamente. O componente a ser fixado não possui rosca e aqui genericamente será denominado de suporte. O terceiro elemento é a porca, cuja rosca é interna. Não por acaso é o único elemento feminino da Junta e, por sua vez, é quem possui maior resistência, no sentido amplo da palavra.

Como todo material possui um determinado módulo de elasticidade, é vedado ao suporte e a porca ultrapassar o regime elástico. As possíveis deformações permanentes no suporte e na porca poderão causar perda de pré-carga. Com relação ao parafuso, este limite (elástico) pode ser superado, sendo permitido que o mesmo seja apertado na sua região elasto-plástica, até nas vizinhas da máxima força tensora que o mesmo pode gerar (e antes da estricção).

Classe de Resistência

O foco será nos Parafusos, pois como citado nos parágrafos anteriores, tanto o suporte como a porca são mais resistentes que o parafuso, assim sendo, o parafuso é o "fusível" deste sistema. E óbvio, ele não pode "queimar". Quanto maior a classe de resistência, por exemplo 12.9, maior será a capacidade de geração de força por este elemento de fixação.

Classes 8.8, 9.8, 10.9 e 12.9 implicam em transformação térmica do material, processo que envolve aquecimento e principalmente resfriamento. O processo térmico provoca transformações alotrópicas (ferro gama – ferro alfa), com aumento de volume, o que acarreta uma concentrações de tensões, daí a necessidade de revenimento. Mas são estas tensões internas residuais que agregam as propriedades desejadas. Classes inferiores a 8.8 (6.8, por exemplo) não requerem tratamento térmico, porém a resistência destes parafusos são bem menores.

Assim sendo, uma maior classe de resistência implica em maior capacidade de geração de força, conseqüência de maiores tensões residuais internas. Também é um atributo da aplicação do parafuso. Maior tensão residual, maior responsabilidade funcional do parafuso.  

Uma maneira lúdica de fixar o conceito acima descrito é mostrado na Figura 1, onde temos uma Escala Empírica de Tensões Residuais, que denomino como "Síndrome dos Botões da Camisa do Gordinho”, elencando a classe de resistência à responsabilidade do parafuso.  

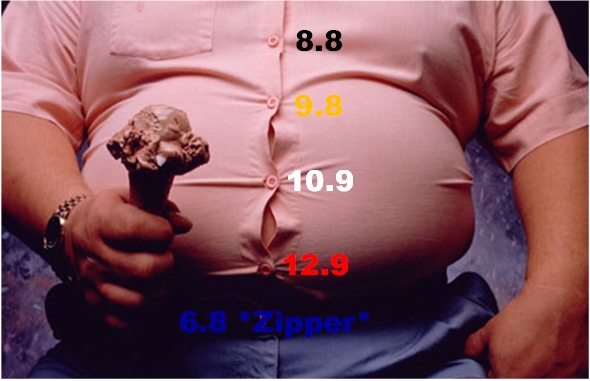
Figura 1: Diagramação "jocosa" associando a classe de resistência de um parafuso para sua responsabilidade funcional.

Maior responsabilidade implica numa classe de resistência mais elevada, e maiores tensões residuais internas.

Esforço Combinado

Ao se apertar um parafuso, o mesmo sofre concomitantemente esforços axiais e torsionais, diferentemente quando se traciona um parafuso, onde temos apenas carga axial pura.

O esforço combinado resulta numa força menor do que a carga axial e este rendimento (η) é inversamente proporcional ao Coeficiente de Atrito de Rosca (μG), como mostra a equação 1 abaixo:

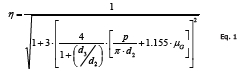
Para aquilatar o quanto μG afeta o η, considerando um parafuso M12 × 1,5, para μG de 0,06 o η é de 92,65%, e para μG de 0,18, η é da ordem de 74,12%. Nesta última condição, praticamente 1/4 (um quarto) do Parafuso vai para o "lixo".  

Força de União

Considerando o esforço combinado e aperto no regime elástico do parafuso, podemos afirmar que o parafuso se comporta como uma mola, logo respeita a Lei de Hooke. O limite do regime elástico é o Limite de Escoamento, também denominado "Yield Point".

A Figura 2 mostra a força de união, gerada por um parafuso, em função da deformação, no regime elástico, cujo limite superior é o "Yield Point".

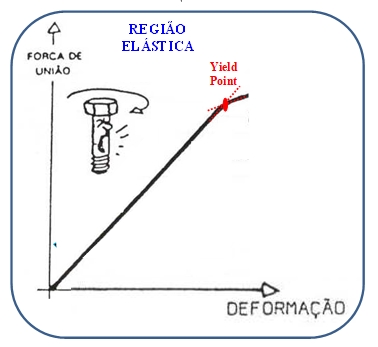
Figura 2: Diagramação mostrando a região elástica do parafuso, cujo limite é o "Yield Point", neste intervalo de força e deformação, o parafuso se comporta como uma mola.

Como estamos no regime elástico, podemos determinar a constante de mola, através da Lei de Hooke.

A expressão que relaciona a Força com o ângulo de aperto é mostrada na equação 2 abaixo:

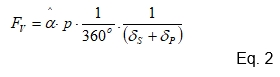
 Re-escrevendo a equação 2 , temos uma expressão que relaciona o ângulo de aperto, as resiliências e a força tensora. Veja a equação 3:

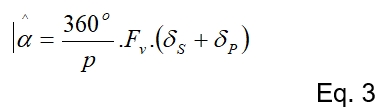
onde: Fv = Força Tensora

δS = Resiliência do Elemento de Fixação

δP = Resiliência da Junta

360º= Constante geométrica, fator de conversão de    p deformação angular em deformação linear.

Convém ressaltar que as equações 2 e 3 só são válidas no regime elástico, ou seja, até o "Yield Point".  

O comportamento de um parafuso, desde o inicio do seu aperto até a sua força máxima, respeita a equação matemática atribuída a Richards, ou seja, trata-se de um comportamento sigmóide, isto é, em formato de sigma (maiúsculo), função assintótica ao eixo de deformação angular, nos limites inferiores de força, quando esta tende a zero, e nos limites superiores de força, quando tende à força máxima. A expressão matemática da Equação de Richards é mostrada na equação 4.

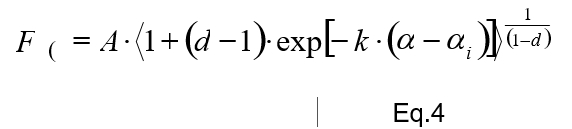
onde:

F(α) = Força Tensora para um dado ângulo (α) de aperto

A = Fator pré-exponencial, relacionado com o valor da força máxima

d = Parâmetro associado à posição do ponto de inflexão ao longo da curva

k = Taxa intrínseca (constante) de crescimento da curva

αi = Ângulo de inflexão da curva sigmoide.

O valor da força no ponto de inflexão ( αi ) é dado pela equação 5:

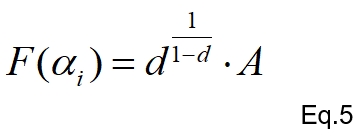
Já o comportamento gráfico representativo da Equação de Richards, para um parafuso M12 X 1,75, 12.9, é mostrado na Figura 3.

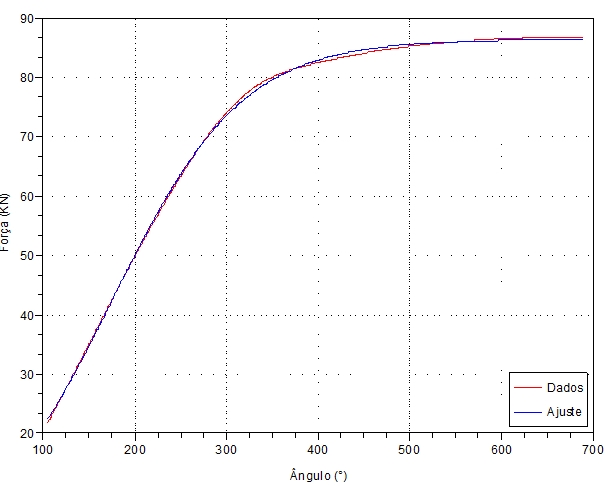
Figura 3: Comportamento gráfico da Equação de Richards. O segmento sigmóide inferior, para força tendendo a zero foi suprimido, pois além de ser assintótico ao eixo da deformação angular, é irrelevante para forças inferiores a 20 k N (M12 X 1,75, 12.9)

Resumindo, se o aperto ocorre na zona elástica do parafuso, o comportamento é linear, respeitando a Lei deHooke. Se o aperto ultrapassa o "Yield Point", adentrando na zona elasto-plástica do parafuso, o comportamento é sigmóide, obedecendo às premissas da expressão matemática atribuída a Richards.

Torque

A ênfase até aqui foi o parafuso como provedor de força tensora. Mas no dia-a-dia é muito mais comum monitorar o torque, a energia utilizada num processo de aperto. A relação entre Torque e Força é dada pela equação 6, mostrada abaixo, denominada Equação Básica.

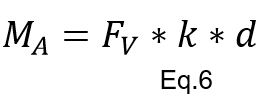
onde:

MA = Torque (Momento de Aperto), expresso em Nm, sistema SI

FV = Força Tensora, expressa em k N (SI)

k = Fator de Torque, "kfactor", adimensional (que é geralmente tabelado e considerado constante)

d = Diâmetro nominal do elemento de fixação, expresso em mm.

A representação gráfica da equação 6 é mostrada na Figura 4, a partir de dados reais, de um parafuso M16 X 2,0, 10.9.

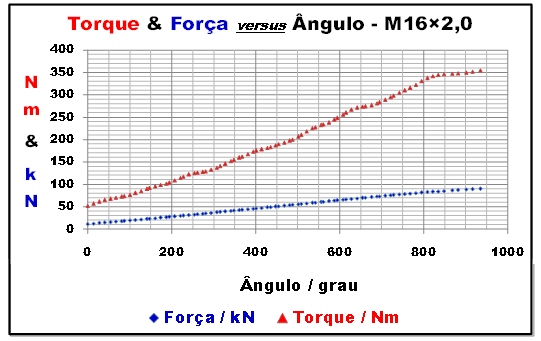
Figura 4: Representação gráfica da Equação Básica de Torque, a partir de dados reais de um parafuso M16 X 2,0, 10.9.

Dr. Roberto Garcia

• Consultor técnico, bacharel em química, mestre e doutor em físico química pela UNESP (Universidade Estadual Paulista), onde é pesquisador colaborador do GEMAT - Instituto de Química (roberto.2.garcia@gmail.com). • Mentor na Assahi Maquinas e Equipamentos Ltda. - Fastening Tecnologies Division (garcia@assahimaquinas.com.br).

A segunda parte deste artigo será publicada em nossa próxima edição.